Enhancing Chaos in some New Class of Dissipative Dynamical Systems
M. A. Aziz Alaoui
Depart. of Math., L.M., Le Havre University
Preprint Le Havre Univ.
Abstract
We report the finding of multispiral chaotic attractors in
some new piecewise-linear system of differential equations of the type
Sprott.
A brief discussion about equilibrium points and their stability is given.
Some of the fundamental routes to chaos and bifurcation phenomena
are demonstrated with various examples.
Introduction
The new notions of chaotification
(also called anticontrol of chaos) has recently attracted much attention.
Chaotification arises when one makes a nonchaotic dynamicl
system chaotic or enhances the existing chaos of a chaotic
dynamical system.
In this contribution, using some piecewise linear
dynamical systems such as Sprott
equations, we show that modification of the
piecewise-linear function enhance the existing chaos,
leading to various `multispiral' strange attractors of a new type.
These attractors appear as a result of the combination of
several `one-spiral' attractors similar to Rossler's.
This is illustrated by some numerical results describing how
the dynamic changes and gives rise to `multispiral attractor'
as the number of segments of the piecewise-linearity increases.
Bifurcation phenomena and transition from order to
`multispiral-chaos' are investigated.
The Mathematical Model :
X''' + A X'' + X' = G(X)
where G is some nonlinear function, A a parameter.
Typical multispiral strange attractors exhibited by this system
are displayed below.
![[IMAGE]](azspr6_nl1.gif)
A 6-spiral strange attractor exhibited by this system
![[IMAGE]](azspr8_nl1.gif)
A 8-spiral strange attractor exhibited by this system
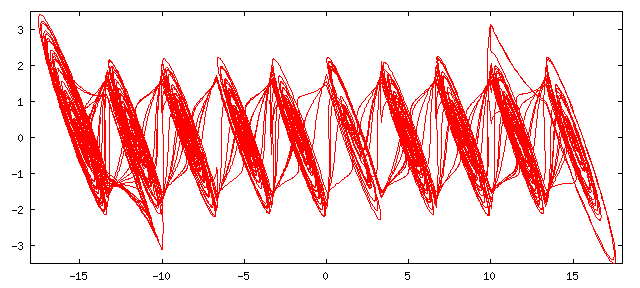
a 10-spiral attractor
Back to the previous page
Back to Aziz Alaoui's home page