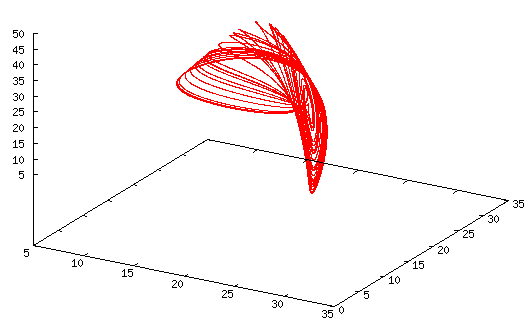
Typical strange attractor exhibited by this system.
Chaos Sol. & Fractals, Vol. 14(issue 8), pp. 1275-1293, (2002).
In this paper we are interested in a three-dimensional system of autonomous differential equation, modeling common ecological situations and taking into account some essential features of the dynamics of some systems in natural settings. Most of the studies on ecosystem models concentrate on Lotka-Volterra or Holling type while the model we study here is based also on Leslie-Gower scheme. Furthermore there are many results on single or two-species models, especially concerning global stability, while biological populations do not exist in isolation. Given some reasonable restrictions on the model, we determine the conditions and establish results for boundedness and local or global stability of equilibria. A rapid study near the xy-plane is also done and a numerical qualitative analysis of the asymptotic behavior of the system is performed. Indeed, recent studies have begun to indicate that chaotic dynamic may play an important role in continuous time models in ecology. Our intensive numerical study goes in the same direction and suggests that natural terrestrial systems may be suitable candidates for researching chaos, even though the regions of parameters, in which the dynamic is chaotic, can be small. The transition behavior when some parameters of the system vary is also studied. Chaotic behavior is observed via sequences of period-doubling bifurcation of limit cycles (in a relatively broad range of parameters) which, however, break down and reverse, giving rise to a sequence of distinctive period-halving. In the present work, the regions of parameters chosen for numerical experiments contain parametric values which are not arbitrary but are quantitative measures of the system attributes. This paper is organized as follows. In section 2, the model is described and rescaling tansformations to obtain simpler analytical form are given. In section 3, the boundedness of the solutions of this system is established. The equilibria and their stabilities are the subject of section 4, a study near the xy-plane is used. The question of existence of chaos is numerically studied in section 5.
The Mathematical Model :
A three-species food chain model is studied analytically as well as numerically. This model describes a prey population X which serves as the only food for a predator Y. This specialist predator Y is, in turn, the prey of a generalist predator Z, which is assumed to reproduce mostly sexually. Much literature exists on the general problem of food chains. These papers often concern three trophic-level food chains model composed of logistic prey X and Lotka-Voltera or Holling type II predator Y and superpredator Z. In this paper, the interaction between species Y and its prey X has been modeled by the Volterra scheme (predator population dies out exponentially in the absence of its prey). But, the interaction between species Z and its prey Y has been modeled by the Leslie-Gower scheme (the loss in a predator population is proportional to the reciprocal of per capita availability of its most favourite food). Furthermore, the predator Z is assumed to reproduce mostly sexually. The general mathematical model will take the form : dX/dT = XF(X,Y), dY/dT = YG(X,Y,Z), dZ/dT = Z^2H(Y) .

Typical strange attractor exhibited by this system.
![]() Back to the previous page
Back to the previous page
Back to Aziz Alaoui's home page