M.A. Aziz Alaoui
Professeur de Mathématiques, Université du Havre, Normandie

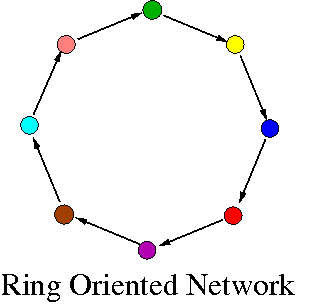
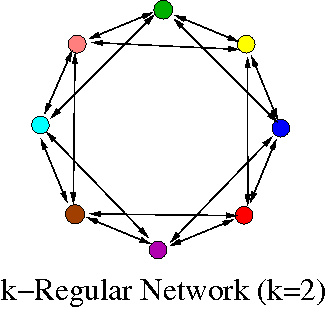
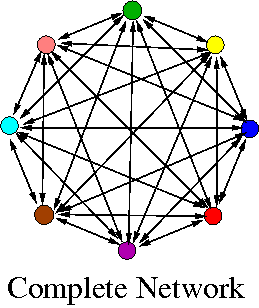
Various Animations of Attractors or patterns

Below, I run different patterns or attractors that we found in differential equations (PDE or ODE) or discrete mappings ... :

Predator-prey diffusif model, rectangular domain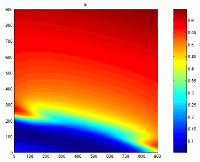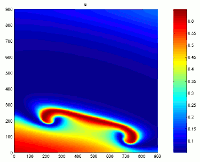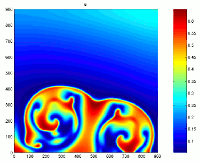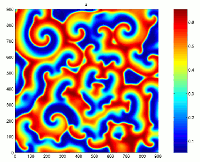

Spatial dynamics (and patterns), on a square domain, of a predator-prey diffusif model with Holling-type-II and a modified Leslie-Gower functional responses. (1) The spatial disperion of the prey, (2) The spatial disperion of the predator.

The renderings are based on models of reaction-diffusion equations which express conservation of predator and prey densities, it has the following form :

\frac {\partial H}{\partial T} = D_1\Delta H + ( a_1 - b_1H -\frac{c_1P}{H+k_1} H

\frac{\partial P}{\partial T} = D_2 \Delta P + a_2 - \frac{c_2P}{H+k_2} P

Predator-prey diffusif model, circular domain

*

Spatial dynamics (and patterns), on a circular domain, of te same predator-prey diffusif model. (1) The spatial disperion of the prey, (2) The spatial disperion of the predator.

See:

For this functionnal response :

- Aziz-Alaoui M.A. (2002), Study of a Leslie-Gower-type tritrophic population model Chaos Sol. & Fractals, Vol. 14(8), pp: 1275-1293, *

See also :

- Aziz-Alaoui M.A. and Daher M.O.(2002), On the dynamics of a predator-prey model with the Holling-Tanner functional response, book-chapter in Mathematical Modelling and Computing in Biology and Medecine, MIRIAM Editions, Editor V. Capasso, pp: 270-278, (2002). *

- Aziz-Alaoui M.A. and Daher M.O.(2003), Boundedness and global stability for a predator-prey model with modified Leslie-gower and Holling-type II schemes, Applied Math. Lets. Vol. 16(7), pp. 1069-1075, *

- The theses of two of my former PhD students (B. Camara and Daher M.O.).

- Camara B.I. and Aziz-Alaoui M.A. (2009), Turing and Hopf Patterns Formation in a Predator-Prey Model with Leslie-Gower-Type Functional Response, Dynamics of Continuous, Discrete and Impulsive Systems, series B, Vol. 16(4), pp: 479-488. *

- Camara B.I. and Aziz-Alaoui M.A. (2008), Dynamics of a Predator-prey model with diffusion, Dynamics of Continuous Discrete and Impulsive Systems, Series A : Mathematical Analysis, Vol. 15, pp: 897-906. *

- Camara B.I. and Aziz-Alaoui M.A. (2008), Complexity in a prey predator model, ARIMA, Vol. 9, pp: 109-122. *

Neurones synchronization

<object style="width:220px;height:178px"> <!param name="movie" value="player.swf?file=video_ns_2.flv" /> <!param name="quality" value="high" /> </object> <object style="width:220px;height:178px"> <!param name="movie" value="player.swf?file=video_fs_2.flv" /> <!param name="quality" value="high" /> </object> <object style="width:220px;height:178px"> <!param name="movie" value="player.swf?file=video_bs_2.flv" /> <!param name="quality" value="high" /> </object>

Movies showing, for 4 coupled Hindmach-Rose systems (modeling 4 coupled neurones), the situation in which 1) no synchronization occurs, 2) complete synchronization and 3) burst synchronization.

See:

- The thesis of one of my former PhD students (N. Corson).

- Corson N., Aziz-Alaoui M.A. (2009), Asymptotic Dynamics for Slow-Fast Hindmarsh-Rose Neuronal System, Dynamics of Continuous, Discrete and Impulsive Systems, series B, Vol. 16(4), pp: 535-549, *

- Corson N., Aziz-Alaoui M.A. (2009), Complex emergent properties in synchronized neuronal oscillations, book chapter, in : From System Complexity to Emergent Properties, A.-A. M. and C. Bertelle (eds.): Understanding Complex Systems, Springer-Verlag, Heidelberg, pp 243-259, *

- Corson N., Balev S., Aziz-Alaoui M.A. (2010), Detection of Synchronization Phenomena in Networks of Hindmarsh-Rose Neuronal Models, Proc. of EPNACS'2010, ECCS'10 European Conference on Complex Systems, Lisbon (Portugal), 13-17 septembre 2010, pp: 1-6, *

- Corson N., Balev S., Aziz-Alaoui M.A. (2011), Burst Synchronization of Coupled Oscillators, Towards Understanding the Influence of the Network Topology, Proc. of EPNACS'2011, Vienna (Autriche), 11-16 septembre 2011, pp: 3-9, *

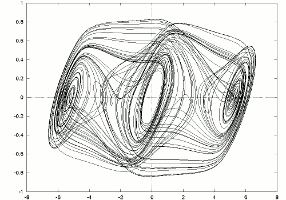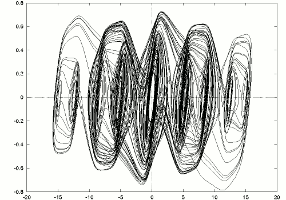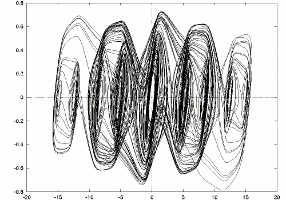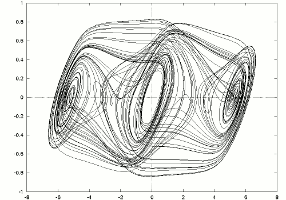
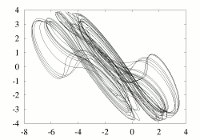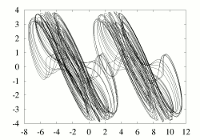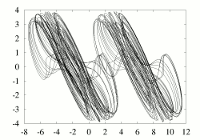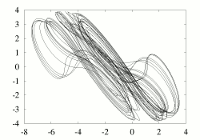
We mainly studied (but nont only) the cases for which the network topology is :

Animated view of multi-scroll attractors

See my paper :

Ref: IJBC 9(6) ,

in the Int. Journ. of Bifurcation and Chaos 9(6), 1009-1039, (1999), (IJBC).

The state equations of Chua's system are given by

dx/dt = alpha.[y-x-f_2(x)], dy/dt = x - y + z, dz/dt = -beta.y -gama.z,

where x, y and z are functions of t, f_2(x)= m_1.x + (1/2)(m_0-m_1)[|x+1|-|x-1|] is the Chua's nonlinearity, which is, here, modified to get multispiral attractors, and alpha, beta, gama, m_1 and m_2 are the parameters of the system.

Animated view of multi-scroll attractors obtained from a non-autonomous differential system

See my paper :

Ref: IJBC 9(6) ,

in the Int. Journ. of Bifurcation and Chaos 9(6), 1009-1039, (1999), (IJBC).

The state equations I used are given by :

dx/dt = y - f_2(x), dy/dt = -alpha*(x + y) +alpha*K*sin(2*PI*Omega*t),

where x and y are functions of t, f_2(x)= m_1.x + (1/2)(m_0-m_1)[|x+1|-|x-1|] is the Chua's nonlinearity, which is, here, modified to get multispiral attractors, and alpha, K, Omega, m_0 and m_1 are the parameters of the system.

Animated view of multi-scroll attractors : a simple dissipative Dynamical (jerk) System

See : "Enhancing Chaos in some New Class of Dissipative Dynamical Systems" (Aziz-Alaoui M.A. unpublished paper, 2001).

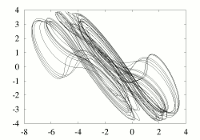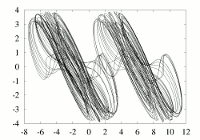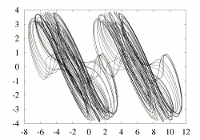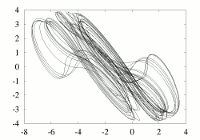
See HERE .

The state equations are given by

x''' + A x'' + x' = G(x),

that is :

dx/dt = y ; dy/dt = z ; dz/dt = -A z + y + G(x) ;

where x, y and z are functions of t, is the nonlinearity I used and modified to get multispiral attractors ...

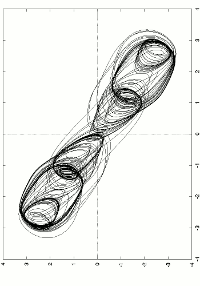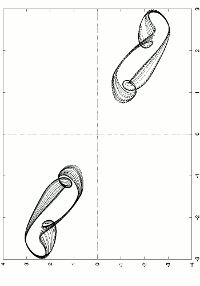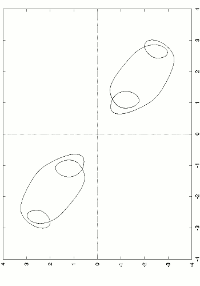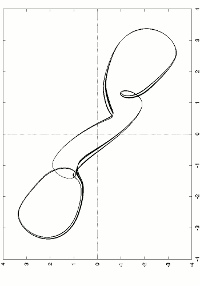
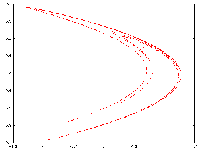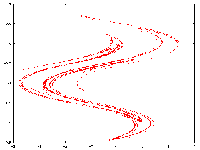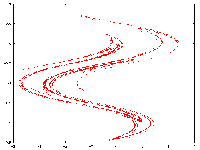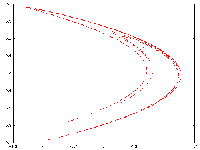
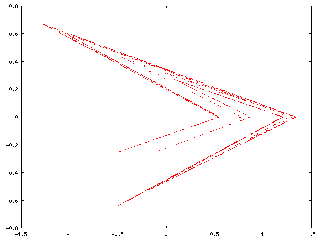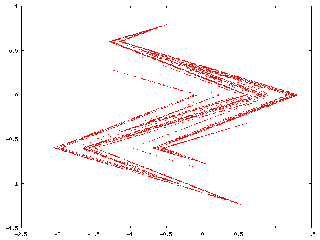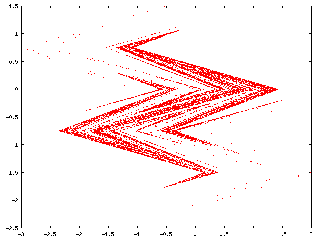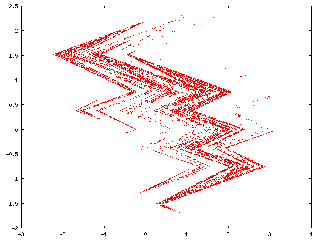
Animated view of a mapping attractor

Appearance of the strange attractor of the mapping which we study in the references cited below (it is a mapping of the type Hénon-Lozi). To see the effect of repeated application of this transformation, we take an arbitrary shape (a square digitized by an array of 100 by 100 regularly spaced points), and apply the transformation iteratively, (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 times). The square is fastly deformed, after a few iterations the attractor becomes recognizable. The following iterations do not have any effect on it . It is a subset of the plane which is invariant with respect to the transformation.

See the papers:
* Dynamics of a Hénon-Lozi type map in Chaos Solitons and Fractals, Vol. 12(12), 2323-2341, (2001)
* Sur une approximation $C^1 d'un endomorphisme linéaire par morçeaux sur le plan unpublished (2001)

Animated view of a Hénon-type mapping attractors

Abstract We present and analyze a modified version of Hénon map. Hénon [1976] studied the following map :

x_{n+1} = y_n+1-a.x_n^2 ,

y_{n+1} = b.x_n

(a and b are the parameters). By modifying the nonlinear term of this map, we obtain some new strange attractors with many folds (interest: secure communication for example ... ! ). The animation shows first the classical Hénon attractor, then a 2-folds strange attractor exhibited by the modified Hénon's map, then a 3-folds strange attractor, then a 4-folds strange attractor.

unpublished papers (published on this site in 1998), See HERE.

Animated view of Lozi-type mapping attractors

Abstract We present and analyze a modified version of Lozi map. Lozi [1978] studied the following map :

x_{n+1} = y_n+1 - a.|x_n| ,

y_{n+1} = b.x_n

(a and b are the parameters). By modifying the nonlinear term of this map, we obtain some new chaotic attractors with many folds (interest: secure communication for example ... ! ). The animation shows first the classical Lozi attractor, then a 2-folds strange attractor exhibited by the modified Lozi's map, then a 3-folds strange attractor, then a 4-folds strange attractor.

unpublished papers (published on this site in 1998), See HERE.